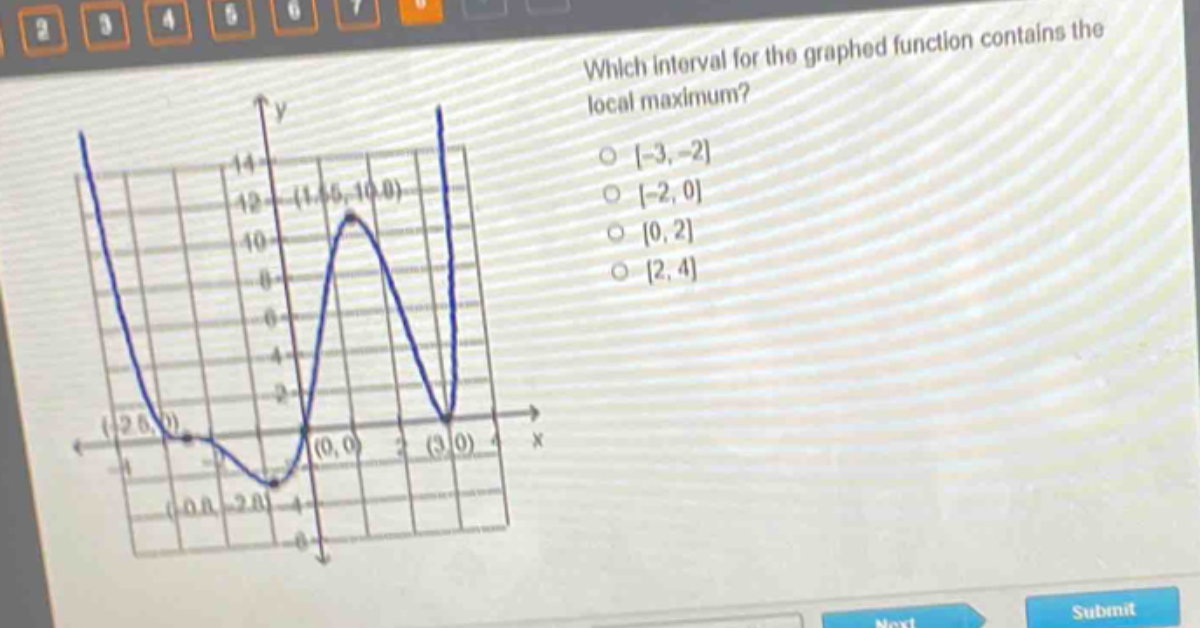
When analyzing a graphed function, one of the most important concepts is identifying the local minimum. A local minimum occurs when the function reaches its lowest point within a particular interval, meaning that no nearby points have a lower value. Understanding which interval for the graphed function contains the local minimum can provide insights into the behavior of the function and help solve various mathematical problems. By examining the graph carefully and considering the changes in the slope, it’s possible to determine where this critical point lies.
What is a Local Minimum?
Definition of Local Minimum
In mathematical terms, a local minimum is the point on a graph where a function changes direction from decreasing to increasing. At this point, the function has a value that is lower than any other nearby points, making it the lowest point in that particular region of the graph. It’s important to note that this is not necessarily the lowest point overall, but rather the lowest point within a specific interval, hence the term “local.”
Local minima are identified by looking at the curve of the graph. If the function is decreasing on an interval and then starts increasing again, the point where it shifts from decreasing to increasing is considered a local minimum.
How to Identify the Local Minimum on a Graphed Function
Examining the Slope of the Graph
To determine which interval for the graphed function contains the local minimum, you need to look at how the function behaves between different points. Specifically, focus on the slope of the curve:
- Decreasing Slope: The function is decreasing when the slope of the graph is negative (sloping downward).
- Increasing Slope: The function is increasing when the slope of the graph is positive (sloping upward).
The local minimum will occur at a point where the graph stops decreasing and begins increasing. This change in the slope direction indicates the location of the local minimum.
Intervals and Critical Points
An interval refers to a specific section of the graph, often denoted as a range of x-values, such as (a, b). To identify the interval that contains the local minimum, look for:
- A section where the graph first decreases and then increases.
- The lowest point within this interval, which is the local minimum.
For example, if a function is decreasing between the interval (1, 4) and starts increasing again after x = 4, then the local minimum is at x = 4, and the interval that contains the local minimum is likely to be (1, 4).
Using Derivatives to Find Local Minima
First Derivative Test
In calculus, the first derivative of a function provides valuable information about the slope of the graph. By taking the derivative of the function, you can identify critical points—places where the slope is zero or undefined. These points are potential candidates for local minima or maxima.
To use the first derivative test:
- Take the derivative of the function.
- Find where the derivative equals zero (f'(x) = 0). These points are where the slope is flat, and the function might change direction.
- Analyze the sign of the derivative before and after the critical point:
- If the derivative changes from negative (decreasing) to positive (increasing) at a point, this point is a local minimum.
Second Derivative Test
The second derivative of a function helps confirm whether a critical point is a local minimum or maximum. If the second derivative at the critical point is positive (f”(x) > 0), the function is concave up, indicating that the point is a local minimum. This test further solidifies which interval contains the local minimum by providing insight into the curve’s concavity.
Practical Examples
Example 1: Polynomial Function
Consider a graphed polynomial function that decreases between the interval (-2, 1) and then begins increasing from x = 1 onwards. The local minimum occurs at x = 1 because this is the point where the function changes direction. Therefore, the interval containing the local minimum is (-2, 1).
Example 2: Trigonometric Function
For a sine function, which oscillates between intervals of increasing and decreasing values, the local minima occur periodically. By looking at the intervals where the sine wave dips to its lowest points, you can identify which sections of the graph contain the local minima. For instance, if the sine function reaches a minimum at x = π, the interval leading to this minimum might be (0, π).